Калибровочная инвариантность уравнений Максвелла.
Если заданы потенциалы 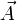 и
и 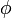 , то этим, согласно
, то этим, согласно
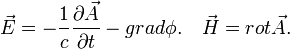
вполне одназначны определены 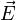 и
и 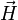 , а значит и поле. Однако одному и тому же полю могут соответствовать различные потенциалы. Чтобы убедиться в этом, прибавим к каждой компоненте потенциала
, а значит и поле. Однако одному и тому же полю могут соответствовать различные потенциалы. Чтобы убедиться в этом, прибавим к каждой компоненте потенциала 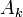 величину
величину 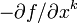 , где
, где 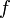 - произвольная функция от координат и времени. Тогда потенциал
- произвольная функция от координат и времени. Тогда потенциал 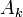 переходит в
переходит в
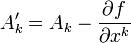 .
.
При такой замене в интеграле действия появится дополнительный член, представляющий собой полный дифференциал:
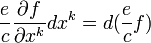 ,
,что не влияет на уравнение движения.
Если вместо четырехмерного потенциала ввести векторный и скалярный и вместо координат 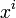 - координаты
- координаты 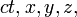 то четыре равества можно записать написать в виде
то четыре равества можно записать написать в виде
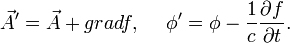
Вид 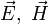 не изменяются.
не изменяются.
Эту инвариантность называют калибровочной или градиентной.