Сказать "Спасибо"
Запаздывающие потенциалы.
Займемся изучением переменных полей при наличие произвольно движущихся зарядов.
Выведем уравнения, определяющие потенциалы поля, создаваемого движущимися зарядами. Надо использовать вторую пару уравнений Максвелла
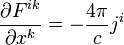
с отличной от нуля правой частью. Такая же правая часть появится и в уравнении
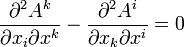
и после наложения на потенциалы условия Лоренца
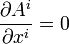 , т.е.
, т.е. 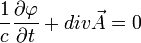
получим
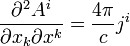
Это и есть уравнение, определяющее потенциалы произвольного электромагнитного поля. В трехмерном виде оно записывается в виде двух уравнений - для 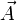 и для
и для 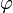 :
:
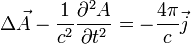 ,
,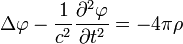 .
.
Для нахождения решения этого частного интеграла разделим все пространство на бесконечно малые участки и определим поле, создаваемое зарядом, находящимся в одной из таких элементов объема. Вследствие линейности уравнений истинное поле будет равно сумме полей, создаваемых всеми такими элементами. Нам надо решить уравнение
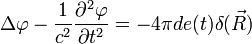
Общее решение имеет вид
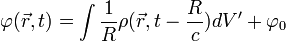 ,
,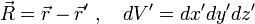 ,
,где 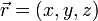 ,
, 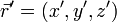 ;
; 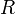 есть расстояние от элемента объема
есть расстояние от элемента объема 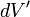 до "точки наблюдения", в которой мы ищем значение потенциала.
Аналогичным образом имеем для векторного потенциала:
до "точки наблюдения", в которой мы ищем значение потенциала.
Аналогичным образом имеем для векторного потенциала: