Сила радиационного трения.

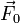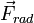Рассмотрим движение нерелятивистской частицы под действием внешней силы $\vec{F}_0$ . Для учета реакции на излучении добавим в правую часть уравнения движения эффективную силу $\vec{F}_{rad}$ :

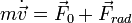
$m\dot{\vec{v}}=\vec{F}_0+\vec{F}_{rad}$

Сконцентрируем эту силу таким образом, чтобы её работа за единицу времени (т.е. мощность) была бы равна энергии излучаемой частицей за единицу времени

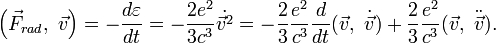
$\left(\vec{F}_{rad},~\vec{v}\right)=- \frac{d\varepsilon}{dt}=- \frac{2e^2}{3c^3}\dot{\vec{v}^2}=- \frac{2}{3} \frac{e^2}{c^3} \frac{d}{dt}(\vec{v},~\dot{\vec{v}})+ \frac{2}{3} \frac{e^2}{c^3}(\vec{v},~\ddot{\vec{v}}).$

Строго это равенство удовлетворить невозможно. Но, если движение частицы финитное, то при усреднении полная производная по времени зануляется, и мы можем записать закон сохранения энергии:

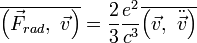
$\overline{\left(\vec{F}_{rad},~\vec{v}\right)}= \frac{2}{3} \frac{e^2}{c^3}\overline{\left(\vec{v},~\ddot{\vec{v}}\right)}$

Следовательно можно выбрать

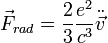
$\vec{F}_{rad}=\frac{2}{3} \frac{e^2}{c^3} \ddot{\vec{v}}$

Это величина называется Лоренцовской силой радиационного торможения.

Сказать "Спасибо"

Сила радиационного трения.

Комментарии