Сказать "Спасибо"

10.
Линейные формы. Сопряженное (двойственное) пространство.
Определение
функции. Мы будем рассматривать линейное пространство L
, вещественное или комплексное. Слово "число"- комплексное
для комплексного пространства и вещественное - иначе.
Определение. Будем
говорить, что на линейном пространстве L задана функция
f от одного вектора, если каждому вектору х принадлежащему
L сопоставлено число
f(x), а также, что задана функция g от двух векторов, если каждой
упорядоченной паре векторов х, у из L
сопоставлено число g(x,y).
Функции на
бесконечномерных пространствах, элементы которых сами являются
функциями, называют функционалами.
Пусть пространство L
имеет размерность n. При выбранном
базисе каждому вектору х из L сопоставлены n
его компонент x1, ...,xn.
При выбранном базисе функция f на линейном
пространстве L задается функцией от n
переменных, определенной на множестве всевозможных наборов x1,
...,xn.
Если базис изменится, тому же вектору х будут соответствовать новые
компоненты, и, следовательно, прежняя функция f будет задана новой
функцией от n переменных.
Определение.
Функция f на линейном пространстве L называется
линейной, если для любых х и у из L и любого числа а
выполнены равенства
1(x + y)=f(x)+f(y), f(ax)=af(x).
Это в
точности то же самое, что линейное отображение L в
одномерное арифметическое
пространство.
Функция,
сопоставляющая каждому вектору число 0,
линейная. Функция, сопоставляющая всем векторам одно и то же число,
отличное от нуля, не линейная, так как для каждой линейной функции f
(0) = 0.
Рассмотрим n-мерное
линейное пространство L и выберем в нем базис
e1,...,en. Значение
линейной функции f на векторе х может быть выражено через координаты
этого вектора x1, ...,xn:
f(х) = f(x1e1
+.. + xnen)=
x1 f(e1)+
... + xn
f(en)
Числа f(e1),
..., f(en)
не зависят от вектора x, а определяются
только функцией f и базисом. Мы доказали следующее Предложение.
Каждая линейная функция на n-мерном
линейном пространстве в произвольном базисе е задается линейным
однородным многочленом x1φ1
... + xn
φn от
координат вектора в этом базисе. Коэффициенты многочлена φ1,...,
φn равны значениям функции на базисных векторах.
Значения функции f на векторах базиса е удобно называть
компонентами или коэффициентами функции f в базисе е. Матрица
линейного отображения n-мерного пространства в одномерное имеет
размеры 1 х n, т. е. это — строка
длины n.
Формула функции в матричном виде записывается так (2й столбец — компоненты вектора х):
![]()
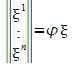 .
.
Каждая
строка
![]() по этой формуле определяет линейную
функцию.
по этой формуле определяет линейную
функцию.
В самом деле,
![]() (x
+ y) =
(x
+ y) =
![]() x
+
x
+![]() y
и
y
и
![]() (аx)
= а
(аx)
= а![]() (x).
Из формулы выражения
матрицы отображения в новых базисах через
его старую матрицу и матрицы перехода к новым базисам, так
как в одномерном арифметическом пространстве базис фиксирован раз и
навсегда, для линейной функции верно
(x).
Из формулы выражения
матрицы отображения в новых базисах через
его старую матрицу и матрицы перехода к новым базисам, так
как в одномерном арифметическом пространстве базис фиксирован раз и
навсегда, для линейной функции верно
![]() '=
'=![]() S
.
S
.
Здесь
![]() — строка коэффициентов функции в базисе е, а
— строка коэффициентов функции в базисе е, а
![]() '
—
'
—
строка ее коэффициентов в базисе е' = eS.
Определение.
Суммой линейных функций f и g называется функция h, значение которой
для любого вектора х определяется равенством h(x) = f (x)
+ g(x). Произведением линейной функции f на число а называется
функция g, значение которой на векторе х определяется
как g(x) =
af(x).
Предложение
2. Пусть f и g — линейные
функции, а
![]() и
и
![]() — их строки коэффициентов в некотором базисе е. Тогда сумма f+g
— линейная функция, и ее строка коэффициентов равна
— их строки коэффициентов в некотором базисе е. Тогда сумма f+g
— линейная функция, и ее строка коэффициентов равна
![]() +
+
![]() .
Для произвольного числа а произведение af — линейная функция, и
ее строка коэффициентов есть а
.
Для произвольного числа а произведение af — линейная функция, и
ее строка коэффициентов есть а![]() .
.
Докажем первую часть предложения. Вторая часть доказывается
аналогично. Для произвольного вектора х значения функций записываются
как f(x) =![]() и g(x) =
и g(x) =
![]() .
Тогда значение суммы f + g на том же векторе равно
.
Тогда значение суммы f + g на том же векторе равно
![]() +
+
![]() = (
= (![]() +
+![]() )
)![]() -
Это показывает, что f+g — линейная функция со строкой
коэффициентов
-
Это показывает, что f+g — линейная функция со строкой
коэффициентов
![]() .
.
Предложение
3. Множество L* всех
линейных функций на n-мерном линейном
пространстве L
no отношению к введенным выше линейным операциям представляет собой
n-мерное линейное пространство.
Действительно, существует взаимно однозначное отображение
множества L* на множество строк длины n,
причем сумме функций соответствует сумма строк, а произведению
функции на число — произведение ее строки на это число.
Поскольку аксиомы линейного пространства выполнены для операций со
строками, они будут выполнены и для операций в L*.
Следовательно, L* —
линейное пространство, изоморфное пространству
строк длины n.
Определение.
Линейное пространство L* всех
линейных функций на линейном пространстве L
называется сопряженным для L.
Выберем базис е в пространстве L
и рассмотрим линейные функции
![]() (i
= 1, ...,n), определяемые равенствами
(i
= 1, ...,n), определяемые равенствами
![]() (х)
=
(х)
=
![]() где
где
![]() — i-я координата вектора х. Это
означает, что
— i-я координата вектора х. Это
означает, что
![]() (i,j = 1,...,n)
(i,j = 1,...,n)
или, иначе,
строка коэффициентов функции
![]() есть i-я строка единичной матрицы. Отсюда
легко следует, что функции
есть i-я строка единичной матрицы. Отсюда
легко следует, что функции
![]() ,...,
,...,![]() линейно независимы. Так как пространство L*
n-мерное, эти функции составляют в нем базис.
линейно независимы. Так как пространство L*
n-мерное, эти функции составляют в нем базис.
Определение.
Базис
![]() ,...,
,...,![]() в L*, определяемый написанной выше
формулой, называется биортогональным или взаимным базису
e1,...,en
пространства L.
в L*, определяемый написанной выше
формулой, называется биортогональным или взаимным базису
e1,...,en
пространства L.
Строка
![]() раскладывается по строкам единичной матрицы с коэффициентами
раскладывается по строкам единичной матрицы с коэффициентами
![]() поэтому элемент f пространства L*
со строкой коэффициентов ||φ1,...,φn
|| имеет разложение f=
поэтому элемент f пространства L*
со строкой коэффициентов ||φ1,...,φn
|| имеет разложение f=
![]() .
.
Введем
столбец р, составленный из функций
![]() Теперь
разложение можно переписать в матричной форме: f =
Теперь
разложение можно переписать в матричной форме: f =
![]() *p.
Таким образом, строка координат элемента f из
L* во взаимном базисе р
совпадает с его строкой коэффициентов в исходном базисе
e
*p.
Таким образом, строка координат элемента f из
L* во взаимном базисе р
совпадает с его строкой коэффициентов в исходном базисе
e
пространства L.
Пространство L* —
такое же линейное пространство, как и любое другое, и, следовательно,
имеет сопряженное пространство L**, элементы которого —
линейные функции на L*.
Предложение
4. Пространство L**
может быть отождествлено с L.
Доказательство. Фиксируем определенный вектор х из L
и сопоставим каждому элементу f из
L* число f(x). Таким образом,
х можно рассматривать как функцию на L*.
Эта функция линейная. Действительно, (f + g)(x) = f (x)
+ g(x), и (af)(x) = af(x).
Итак, х
можно отождествить с некоторым элементом L**.
При этом сумма и произведение на число для векторов из L
совпадают с их суммой и произведением на число, если их понимать как
функции на L*. Это очевидно.
Например, для суммы это равносильно равенству f(х
+ у) = f (x) + f(у).
Теперь мы видим,
что L может быть
отождествлено с подпространством в L**.
Но dim L = dim L
* = dim L **, и
подпространство совпадает со всем пространством.
