Сказать "Спасибо"
- № 46 Разложение в степенной ряд
ln(1+x).
- Пусть f(x)=ln(1+x). Тогда
 (21)
(21)- откуда находим
 (22)
(22)
- ○ Оценим остаточный член
 ,при
,при пользуясь формулой
пользуясь формулой
 (t)dt
(9)(остаточный член ф-лы
Тейлора для функции f
в точке
(t)dt
(9)(остаточный член ф-лы
Тейлора для функции f
в точке
 в интегральной форме) .Преобразуем
эту формулу ,полагая
в интегральной форме) .Преобразуем
эту формулу ,полагая
 .Тогда
.Тогда
 ,
, и
формула (9) примет вид
и
формула (9) примет вид
 (23)
(23)- Если f(x)=ln(1+x) ,то по формуле (23) , используя равенство (21),получаем :

 (24)
(24)- Пусть
 .
Тогда справедливы неравенства
.
Тогда справедливы неравенства
 (25)
(25) (26)
(26)- так как
 .Отсюда
следует ,что при любом
.Отсюда
следует ,что при любом
 выполняется
неравенство
выполняется
неравенство (27)
(27)- Используя неравенство (27), из формулы (24) получаем следующую оценку остаточного члена :

- откуда следует ,что
 при
при
 ,
если |x|<1.
,
если |x|<1.- Пусть x=1 . Тогда
 ,
,
 ,
,
 ,
так как
,
так как

- Поэтому из формулы (24) следует ,что
 ,
откуда плучаем
,
откуда плучаем
 при
при
 .
.
- Итак ,если
 ,
то остаточный член
,
то остаточный член
 для
функции f(x)=ln(1+x) стремится
к 0 , при , т. е. ряд Маклорена сходится к f(x).●
для
функции f(x)=ln(1+x) стремится
к 0 , при , т. е. ряд Маклорена сходится к f(x).●- Из формулы
 (ряд
Маклорена) и (22) , получаем разложение функции
(ряд
Маклорена) и (22) , получаем разложение функции
- ln(1+x) в ряд Маклорена :
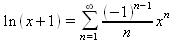 (28)
радиус сходимости которого R=1.
(28)
радиус сходимости которого R=1.- Формула (28) справедлива и при x=1 , и поэтому
 =1–
=1–

- Заменяя в формуле (28) x на (–x) , получаем
 (29).
(29).
- .
- Пусть f(x)=ln(1+x). Тогда
