Сказать "Спасибо"
Отыскание решений линейной неоднородной системы уравнений с постоянными коэффициентами в случае, когда свободные члены уравнений являются квазимногочленами.
Рассмотрим нормальную линейную неоднородную систему
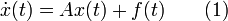
Определение.
Вектор - квазимногочлен называется вектор-функция f(t) = eμtPm(t), где μ - заданное комплексное число, Pm(t) - вектор- многочлен степени m, коэффициентами котрого служат n - мерные векторы.
Теорема.
Если в системе (1)
![f(t)=e^{\mu t}\left[P_m^{(1)}(t)h_1+...+P_m^{(k)}(t)h_k\right]](4_diffur/13/1.png) ,
,где 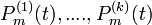 - многочлены степени не выше m, то для системы (1) существует и единственно решение вида
- многочлены степени не выше m, то для системы (1) существует и единственно решение вида
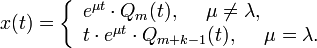
Ищем решение (1) в виде
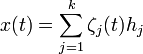 .
.Подставляя в систему (1) и используя определение жордановой цепочки, и в силу линейной независимости h1,...,hk следует, что
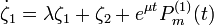
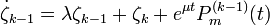
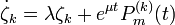
1) при 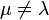 решение этой системы
решение этой системы
2) при μ = λ решение этой системы