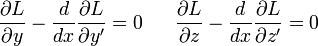Сказать "Спасибо"
Задача Лагранжа (без доказательства).
Рассмотрим интеграл
![J(y, z)=\int_{a}^{b}F[x, y(x), y'(x), z(x), z'(x)]dx~~~~~(1)](4_diffur/21/0.png)
на множестве пар функций (y(x),z(x))
![M=\left\{(y(x), z(x))\in \mathbb{C}_2^1[a, b]:\right.](4_diffur/21/1.png)
![\left.y(a)=A_1, z(a)=A_2, y(b)=B_1, z(b)=B_2, g[x, y(x), z(x)]=0, \forall x\in[a.b] \right\}](4_diffur/21/2.png)
Составим Лагранжиан
L = F[x,y(x),y'(x),z(x),z'(x)] + λ(x)g(x,y,z), где ![\lambda(x)\in \mathbb{C}[a, b]](4_diffur/21/3.png) , называемая неопределенным множителем Лагранжа.
, называемая неопределенным множителем Лагранжа.
Теорема. Пусть дважды непрерывно дифференцируемая функция 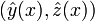 является решением задачи Лагранжа и пусть
является решением задачи Лагранжа и пусть ![\left[\frac{\partial g(x, \hat{y}, \hat{z})}{\partial y}\right]^2+\left[\frac{\partial g(x, \hat{y}, \hat{z})}{\partial z}\right]^2 > 0 \forall x\in [a,b]](4_diffur/21/5.png) . Тогда существует множитель Лагранжа λ(x) такой, что пара функций
. Тогда существует множитель Лагранжа λ(x) такой, что пара функций 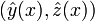 необходимо на [a,b] удовлетворяет системе уравнений Эйлера вида
необходимо на [a,b] удовлетворяет системе уравнений Эйлера вида