Сказать "Спасибо"
Теорема Римана об осцилляции
Теорема.
Функция 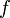 абсолютно интегрируема на конечном или бесконечном интервале
абсолютно интегрируема на конечном или бесконечном интервале 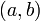 .Тогда
.Тогда
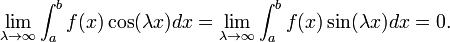
Доказательство.
(*) Будем считать 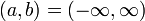 . Функция
. Функция 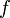 является непрерывной по сдвигу в среднем, т.е.
является непрерывной по сдвигу в среднем, т.е.
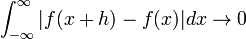 при
при 
Заменим в начальном интеграле 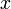 на
на 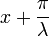 , получаем
, получаем
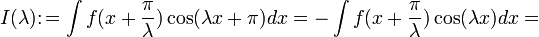
![=-\frac{1}{2}\int\left [ f(x+\frac{\pi}{\lambda})-f(x) \right ]\cos(\lambda x)dx](4_matan/27/d498b3493c2799e5770ce40dd0a040b0.png)
в силу (*) получаем утверждение теоремы.
