Сказать "Спасибо"
Формула Пуазейля.
Пусть вязкая несжимая жидкость течет вдоль прямолинейной цилиндрической трубы радиусом 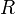 .
.
Выделим в трубе произвольную бесконечно короткую цилиндрическую часть длиной 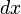 . На её боковую поверхность в направлении движения действует касательная сила
. На её боковую поверхность в направлении движения действует касательная сила
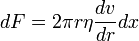
. Кроме того на основания цилиндра в том же направлении действует сила разности давлений
![dF_1=\pi r^2[P(x)-P(x+dx)]=-\pi r^2 \frac{dP}{dx}dx](5_fiz/17/3.png)
При стационарном течении сумма этих двух сил дожна обращаться в нуль, а потому
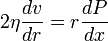
Скорость на стенке обращается в нуль.
Получаем для скорости в зависимости от расстояния от центра
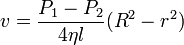
Подсчитаем расход жидкости
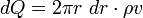
Подставляя сюда выражении для скорости и интегрирую по радиусу получаем

это и есть формула Пуазейля для расхода жидкости.
