Энтропия идеального газа.
Рассмотрим бесконечно малый обратимы процесс. С учетом уравнения состояния идеального газа имеем
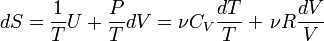
Здесь  - теплоемкость одного моля газа.
- теплоемкость одного моля газа.
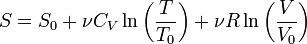
Энтропия идеального одноатомного газа.
Если газ занимает объем 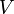 и имеет энергию
и имеет энергию  , то максимальный импульс отдельной молекулы есть
, то максимальный импульс отдельной молекулы есть 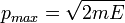 . Тогда фазовая траектория будет расположена на поверхности, являющейся сферой радиуса
. Тогда фазовая траектория будет расположена на поверхности, являющейся сферой радиуса 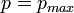 в
в 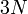 - мерном импульсном пространстве.
Площадь поверхности этой сферы
- мерном импульсном пространстве.
Площадь поверхности этой сферы 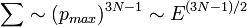 .
Если принять "толщину" слоя равной
.
Если принять "толщину" слоя равной 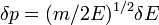 , то объем фазового пространства, занимаемого системой, составит
, то объем фазового пространства, занимаемого системой, составит
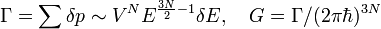 ,
,а для энтропии получаем выражение

(учтено, что 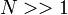 ). Согласно определению температуры имеем
). Согласно определению температуры имеем
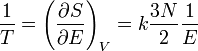 или
или  .
.Это позволяет переписать выражение для энтропии в виде:
