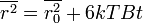Броуновское движение - называется беспорядочное движение малых частиц, находящихся в жидкости или газе, вызванное случайными ударами молекул окружающей среды.

Закон Эйнштейна - Смолуховского. Пусть маленькая частица движется в среде. На неё действуют два типа сил.

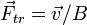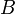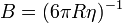1) Сила торможения за счет вязкого трения $\vec{F}_{tr}=\vec{v}/B$ . Величина $B$ называется подвижностью частицы. В частоном случае сферической частицы: $B=(6\pi R\eta)^{-1}$ .

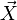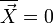2) Флуктуационная (случайная) сила $\vec{X}$ со стороны молекул среды, $\overline{\vec{X}}=0$ .

Запишем уравнение движения частицы:

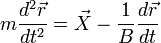
$m\frac{d^2\vec{r}}{dt^2}=\vec{X}-\frac{1}{B}\frac{d\vec{r}}{dt}$

Умножая его почленно на 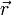$\vec{r}$ и усредняя по большому числу различных частиц, получим

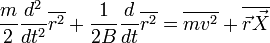$\frac{m}{2}\frac{d^2}{dt^2}\overline{r^2}+\frac{1}{2B}\frac{d}{dt}\overline{r^2}=\overline{mv^2}+\overline{\vec{r}\vec{X}}$ .

Здесь использовано тождество

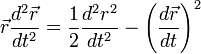
$\vec{r}\frac{d^2\vec{r}}{dt^2}=\frac{1}{2}\frac{d^2r^2}{dt^2}-\left(\frac{d\vec{r}}{dt}\right)^2$

В следствии случайного характера полагаеи 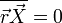$\overline{\vec{r}\vec{X}} =0$ . Учтем также, что в сооответствии с теоремой о равнораспределении энергии по степеням свободы

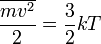$\frac{\overline{mv^2}}{2}=\frac{3}{2}kT$ .

Это приводит к уравнению

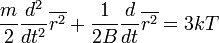
$\frac{m}{2}\frac{d^2}{dt^2}\overline{r^2}+\frac{1}{2B}\frac{d}{dt}\overline{r^2}=3kT$

решение которого имеет вид

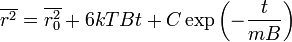
$\overline{r^2}=\overline{r_0^2}+6kTBt+C\exp\left(-\frac{t}{mB}\right)$

на достаточно больших временах получаем закон Эйнштейна-Смолуховского:

$\overline{r^2}=\overline{r_0^2}+6kTBt$

Сказать "Спасибо"

Броуновское движение.

Комментарии