Экзамен по теоретической физике (7 сессия)
Списком
Лекции шестого семестра Суханова (pdf)*Билет 1
1. Принцип суперпозиции состояний. Состояния физической системы как векторы гильбертового пространства.
2. Стационарная теория возмущений для случая невырожденного уровня энергии.
3. Найти дифференциальное сечение рассеяния  - частиц на
- частиц на  - частицах.
- частицах.
Билет 2
1. Линейные эрмитовы операторы в пространстве состояний. Проблема собственных значений и собственных векторов линейных эрмитовых операторов.
2. Стационарная теория возмущений для случая вырожденного уровня энергии. Правильные функции нулевого приближения.
3. Спиновые состояния двух частиц со спином 1/2, отвечающие определенным значениям суммарного спина S.
Билет 3
1. Физическая интерпретация коэффициентов разложения по собственным векторам
2. Нестационарная теория возмущений. Квантовые переходы под влиянием возмущения, действующего в течение конечного промежутка времени
3. Найти время жизни 2p - состояния атома водорода.
Билет 4
1. Условия совместной измеримости физических величин.
2. Квантовые переходы под действием постоянного во времени возмущения. "Золотое правило" Ферми
3. Найти в борновском приближении дифференциальное сечение рассеяния частиц кулоновским полем.
Билет 5
1. Среднее значение и дисперсия физической величины.
2. Критерий применимости квазиклассического приближения. Вид волновой функции в квазиклассическом приближении.
3. Найти вероятность того, что при  - распаде трития ион
- распаде трития ион  окажется в
окажется в 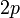 - состоянии.
- состоянии.
Билет 6
1. Соотношение неопределенностей.
2. Эффект Штарка. Линейный эффект Штарка в атоме водорода.
3. Найти отличные от нуля матричные элементы понижающего и повышающего операторов для осциллятора.
Билет 7
1. Координатное и импульсное представление в квантовой механике.
2. Правило квантования Бора-Зоммерфельда. Вероятность проникновения частицы через барьер в квазиклассическом приближении.
3. Вывести правило отбора по полному спину и четности для дипольных переходов в атоме.
Билет 8
1. Оператор эволюции. Представление Шредингера.
2. Уравнение Дирака свободной релятивистcкой частицы. Матрицы Дирака и их свойства.
3. Пользуясь правилами Хунда, определите термы основного состояния атомов: а)углерода, б) азота, в) кислорода.
Билет 9
1. Представление Гайзенберга. Уравнения Гайзенберга для операторов физических величин.
2. Градиентная инвариантность уравнения Дирака.
3. Для частицы в поле вида  найти вероятность "ионизации" при внезапном изменении параметра ямы от
найти вероятность "ионизации" при внезапном изменении параметра ямы от 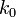 до
до  .
.
Билет 10
1. Производные по времени операторов координаты и импульса частицы в потенциальном поле. Теоремы Эренфеста.
2. Квазивырождение, случай двух близких уровней энергии.
3. Вывести правила отбора по проекции полного момента 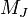 и полного орбитального момента
и полного орбитального момента 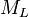 для дипольных переходов в атоме.
для дипольных переходов в атоме.
Билет 11
1. Уравнение непрерывности для плотности вероятности. Плотность потока вероятности.
2. Переходы под действием периодического возмущения в дискретном и непрерывных спектрах.
3. Найти дифференциальное сечение рассеяния протонов на протонах.
Билет 12
1. Оператор изменения во времени физической величины. Интегралы движения. Коммутаторы и скобки Пуассона.
2. Обменное взаимодействие.
3. В представлении, где 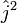 и
и 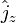 диагональны, найти матрицы операторов
диагональны, найти матрицы операторов  и
и  . Как частный случай получить матрицы Паули.
. Как частный случай получить матрицы Паули.
Билет 13
1. Линейный гармонический осциллятор. Операторы рождения и уничтожения. Энергетический спектр.
2. Решение уравнения Дирака для свободной частицы. Состояния с положительными и отрицательными энергиями.
3. Используя второй порядок стационарной теории возмущений, определите, как зависит потенциальная энергия взаимодействия от расстояния R между атомом и ионом.
Билет 14
1. Коммутационные соотношения для операторов углового момента. Система собственных векторов операторов 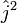 и
и 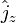 .
.
2. Уравнение Паули как нерелятивистский предел уравнения Дирака.
3. Используя второй порядок стационарной теории возмущений, определите, как зависит потенциальная энергия взаимодействия от расстояния R между двумя атомами.
Билет 15
1. Оператор орбитального момента в координатном представлении. Сферические гармоники.
2. Спин-орбитальное взаимодействие в атоме водорода.
3. Найти в квазиклассическом приближении уровни энергии линейного гармонического осциллятора.
Билет 16
1. Спин частицы. Матрицы Паули.
2. Эффект Зеемана. Эффект Пашена-Бака.
3. Найти собственное значений энергии и собственную функцию связанного состояния в поле  .
.
Билет 17
1. Построение собственных функций осциллятора в координатном представлении с помощью операторов рождения и уничтожения. Связь n - ого состояния с основным.
2. Симметрия волновой функции системы тождественных частиц. Бозоны и фермионы. Детерминант Слэтера. Принцип Паули.
3. Вывести правила отбора по полному моменту  и полному орбитальному моменту
и полному орбитальному моменту 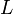 для дипольных переходов в атоме.
для дипольных переходов в атоме.
Билет 18
1. Матричные представления в квантовой механике.
2. Атом гелия. Спиновые функции двух электронов. Пара- и ортосостояния.
3. Элементарная теория  распада. Закон Гейгера-Неттола.
распада. Закон Гейгера-Неттола.
Билет 19
1. Унитарные преобразования векторов состояний и операторов.
2. Постановка задачи рассеяния. Упругое рассеяние. Амплитуда и сечение рассеяния.
3. Записать уравнение Шредингера для двух частиц с массами m1 и m2 взаимодействующих по закону U(r1-r2), а в системе центра масс.
Билет 20
1. Уравнение Шредингера. Стационарные состояния. Статистическая интерпретация волновой функции.
2. Приближение Борна. Критерий применимости борновского приближения.
3. Вычислите энергию основного состояния атома водорода из вариационного принципа. В качестве пробной функции возьмите 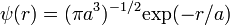 .
.
Билет 21
1. Общая теория движения в поле центрально-симметричного потенциала. Интегралы движения. Радиальное уравнение Шредингера.
2. Адиабатические и внезапные возмущения.
3. Вывести формулу для амплитуды рассеяния в борновском приближении(центрально-симметричное поле)
Билет 22
1. Атом водорода. Дискретные уровни энергии. Собственные функции. Вырождение.
2. Функция Грина задачи рассеяния. Интегральное уравнение для задачи рассеяния.
3. Написать волновую функцию первого возбужденного состояния атома гелия.
- Линейные эрмитовы операторы в пространстве состояний. Проблема собственных значений и собственных векторов линейных эрмитовых операторов.
- Уравнение Шредингера. Стационарные состояния. Статистическая интерпретация волновой функции.
- Уравнение непрерывности для плотности вероятности. Плотность потока вероятности.
- Принцип суперпозиции состояний. Состояния физической системы как векторы гильбертового пространства.
- Физическая интерпретация коэффициентов разложения по собственным векторам
- Среднее значение и дисперсия физической величины.
- Матричные представления в квантовой механике.
- Координатное и импульсное представление в квантовой механике.
- Оператор изменения во времени физической величины. Интегралы движения. Коммутаторы и скобки Пуассона.
- Условия совместной измеримости физических величин.
- Соотношение неопределенностей.
- Оператор эволюции. Представление Шредингера.
- Представление Гайзенберга. Уравнения Гайзенберга для операторов физических величин.
- Общая теория движения в поле центрально-симметричного потенциала. Интегралы движения. Радиальное уравнение Шредингера.
- Оператор орбитального момента в координатном представлении. Сферические гармоники.
- Спин частицы. Матрицы Паули.
- Критерий применимости квазиклассического приближения. Вид волновой функции в квазиклассическом приближении.
- Стационарная теория возмущений для случая невырожденного уровня энергии.
- Стационарная теория возмущений для случая вырожденного уровня энергии. Правильные функции нулевого приближения.
- Нестационарная теория возмущений. Квантовые переходы под влиянием возмущения, действующего в течение конечного промежутка времени.
- Переходы под действием периодического возмущения в дискретном и непрерывных спектрах.
- Квантовые переходы под действием постоянного во времени возмущения. "Золотое правило" Ферми.
- Адиабатические и внезапные возмущения.
- Эффект Штарка. Линейный эффект Штарка в атоме водорода.
- Эффект Зеемана. Эффект Пашена-Бака.
- Правило квантования Бора-Зоммерфельда. Вероятность проникновения частицы через барьер в квазиклассическом приближении.
- Производные по времени операторов координаты и импульса частицы в потенциальном поле. Теоремы Эренфеста.
- Обменное взаимодействие.
- Линейный гармонический осциллятор. Операторы рождения и уничтожения. Энергетический спектр.
- Решение уравнения Дирака для свободной частицы. Состояния с положительными и отрицательными энергиями.
- Коммутационные соотношения для операторов углового момента. Система собственных векторов операторов
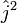 и
и 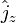 .
.
- Уравнение Паули как нерелятивистский предел уравнения Дирака.
- Спин-орбитальное взаимодействие в атоме водорода.
- Построение собственных функций осциллятора в координатном представлении с помощью операторов рождения и уничтожения. Связь n - ого состояния с основным.
- Симметрия волновой функции системы тождественных частиц. Бозоны и фермионы. Детерминант Слэтера. Принцип Паули.
- Унитарные преобразования векторов состояний и операторов.
- Постановка задач рассеяния. Упругое рассеяние. Амплитуда и сечение рассеяния.
- Уравнение Дирака свободной релятивистcкой частицы. Матрицы Дирака и их свойства.
- Приближение Борна. Критерий применимости борновского приближения.
- Атом водорода. Дискретные уровни энергии. Собственные функции. Вырождение.
- Функция Грина задачи рассеяния. Интегральное уравнение для задачи рассеяния.
- Атом гелия. Спиновые функции двух электронов. Пара- и ортосостояния.
- Квазивырождение, случай двух близких уровней энергии.
- Градиентная инвариантность уравнения Дирака.
Задачи
- Найти дифференциальное сечение рассеяния
 - частиц на
- частиц на  - частицах.
- частицах.
- Используя второй порядок стационарной теории возмущений, определите, как зависит потенциальная энергия взаимодействия от расстояния R между атомом и ионом.
- Найти в квазиклассическом приближении уровни энергии линейного гармонического осциллятора.
- Найти вероятность того, что при
 - распаде трития ион
- распаде трития ион  окажется в
окажется в 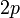 - состоянии.
- состоянии.
- Найти собственное значений энергии и собственную функцию связанного состояния в поле
 .
.
- Найти время жизни 2p - состояния атома водорода.
- Найти в борновском приближении дифференциальное сечение рассеяния частиц кулоновским полем.
- Найти отличные от нуля матричные элементы понижающего и повышающего операторов для осциллятора.
- Найти дифференциальное сечение рассеяния протонов на протонах.
- Для частицы в поле вида
 найти вероятность "ионизации" при внезапном изменении параметра ямы от
найти вероятность "ионизации" при внезапном изменении параметра ямы от 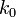 до
до  .
.
- Спиновые состояния двух частиц со спином 1/2, отвечающие определенным значениям суммарного спина S.
- Вывести правило отбора по полному спину и четности для дипольных переходов в атоме.
- В представлении, где
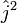 и
и 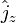 диагональны, найти матрицы операторов
диагональны, найти матрицы операторов  и
и  . Как частный случай получить матрицы Паули.
. Как частный случай получить матрицы Паули.
- Используя второй порядок стационарной теории возмущений, определите, как зависит потенциальная энергия взаимодействия от расстояния R между двумя атомами.
- Элементарная теория
 распада. Закон Гейгера-Неттола.
распада. Закон Гейгера-Неттола.
- Записать уравнение Шредингера для двух частиц с массами m1 и m2 взаимодействующих по закону U(r1-r2), а в системе центра масс.
- Вычислите энергию основного состояния атома водорода из вариационного принципа. В качестве пробной функции возьмите
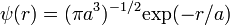 .
.
- Написать волновую функцию первого возбужденного состояния атома гелия.
- Вывести правила отбора по полному моменту
 и полному орбитальному моменту
и полному орбитальному моменту 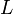 для дипольных переходов в атоме.
для дипольных переходов в атоме.
- Вывести правила отбора по проекции полного момента
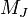 и полного орбитального момента
и полного орбитального момента 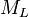 для дипольных переходов в атоме.
для дипольных переходов в атоме.
- Вывести формулу для амплитуды рассеяния в борновском приближении(центрально-симметричное поле)